set_cover

The Set Cover problem is one of the problems in graph theory that tries to solve the least possible set of sets that covers all elements inside those sets. Given a set of n elements, and a collection of m sets containing them, the algorithm tries to identify the smallest sub-collection of sets whose union equal to all the elements. It is NP-complete, however solvable with techniques such as constraint programming. The current algorithm uses GEKKO optimizer as a constraint programming solver.

Trait	Value
Module type	module
Implementation	Python
Graph direction	undirected
Edge weights	unweighted
Parallelism	sequential

Too slow?

If this algorithm implementation is too slow for your use case, contact us and request a rewrite to C++ !

Procedures

info

If you want to execute this algorithm on graph projections, subgraphs or portions of the graph, be sure to check out the guide on How to run a MAGE module on subgraphs.

cp_solve(element_vertexes, set_vertexes)

Input

The input itself represents an element-set pair with each row of the lists.

• element_vertexes: List[Vertex] ➡ List of element nodes in pairs
• set_vertexes: List[Vertex] ➡ List of set nodes in pairs

Output

• containing_set ➡ minimal set of sets in which all the elements are contained

Usage

CALL set_cover.cp_solve([(:Point), (:Point)], [(:Set), (:Set)])
YIELD containing_set;

Example

Step 1: Input graph

Step 2: Cypher load commands

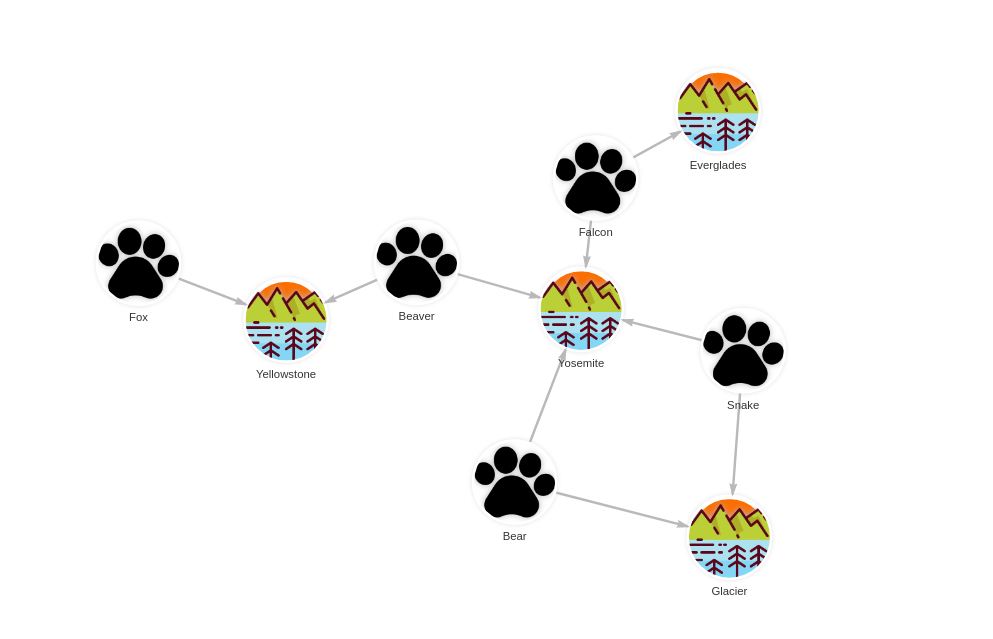
CREATE (e:AnimalSpecies {name: 'Snake'});
CREATE (e:AnimalSpecies {name: 'Bear'});
CREATE (e:AnimalSpecies {name: 'Falcon'});
CREATE (e:AnimalSpecies {name: 'Beaver'});
CREATE (e:AnimalSpecies {name: 'Fox'});

CREATE (s:NationalPark {name: 'Yosemite'});
CREATE (s:NationalPark {name: 'Grand Canyon'});
CREATE (s:NationalPark {name: 'Yellowstone'});
CREATE (s:NationalPark {name: 'Glacier'});
CREATE (s:NationalPark {name: 'Everglades'});

MATCH (e: AnimalSpecies {name: 'Snake'}), (s:NationalPark {name: 'Yosemite'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Bear'}), (s:NationalPark {name: 'Yosemite'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Falcon'}), (s:NationalPark {name: 'Yosemite'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Beaver'}), (s:NationalPark {name: 'Yosemite'})
CREATE (e)-[:LIVES_IN]->(s);

MATCH (e: AnimalSpecies {name: 'Fox'}), (s:NationalPark {name: 'Yellowstone'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Beaver'}), (s:NationalPark {name: 'Yellowstone'})
CREATE (e)-[:LIVES_IN]->(s);

MATCH (e: AnimalSpecies {name: 'Snake'}), (s:NationalPark {name: 'Glacier'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Bear'}), (s:NationalPark {name: 'Glacier'})
CREATE (e)-[:LIVES_IN]->(s);

MATCH (e: AnimalSpecies {name: 'Falcon'}), (s:NationalPark {name: 'Everglades'})
CREATE (e)-[:LIVES_IN]->(s);

Step 3: Running command

MATCH (e:AnimalSpecies)-[l:LIVES_IN]-(s:NationalPark)
WITH collect(e) AS animal_list, collect(s) AS park_list
CALL set_cover.cp_solve(animal_list, park_list)
YIELD containing_set
WITH containing_set AS national_park
MATCH (animal:AnimalSpecies)-[l:LIVES_IN]->(national_park)
RETURN animal, l, national_park;

Step 4: Results

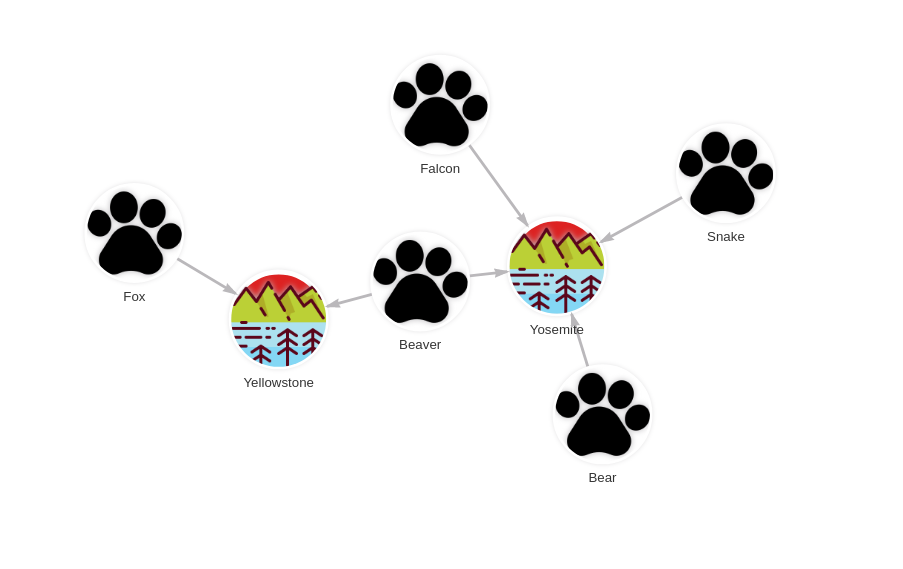
greedy(context, element_vertexes, set_vertexes)

Not bad, not terrible.

Input

The input itself represents an element-set pair with each row of the lists.

• element_vertexes: List[Vertex] ➡ List of element nodes in pairs
• set_vertexes: List[Vertex] ➡ List of set nodes in pairs

Output

• containing_set ➡ minimal set of sets in which all the elements are contained

Usage

CALL set_cover.greedy([(:Point), (:Point)], [(:Set), (:Set)])
YIELD containing_set;