cycles

In graph theory, a cycle represents a path within the graph where only the starting and ending nodes are equal. Furthermore, cycles can be double-connected links between neighboring nodes or self-loops. The cycles detection algorithm implemented within MAGE works on an undirected graph and has no guarantee of node order in the output. The implemented algorithm (Gibb) is described in the 1982 MIT report called "Algorithmic approaches to circuit enumeration problems and applications" ¹. The problem is not solvable in polynomial time. It is based on finding all subsets of fundamental cycles which takes about O(2^(|E|-|V|+1)) time where E represents a set of edges and V represents a set of vertices of the given graph.

¹ Algorithmic approaches to circuit enumeration problems and applications, Boon Chai Lee

Trait	Value
Module type	algorithm
Implementation	C++
Graph direction	undirected
Edge weights	unweighted
Parallelism	sequential

Procedures

info

If you want to execute this algorithm on graph projections, subgraphs or portions of the graph, be sure to check out the guide on How to run a MAGE module on subgraphs.

get()

Output:

• cycle_id ➡ Incremental cycle ID of a certain vertex. There is no guarantee on how nodes are going to be ordered within cycle. The cycle can be represented with a minimum of one ID, where it stands for self-loop.
• node ➡ Vertex object with all properties which is going to be related to the cycle ID it belongs to.

Usage:

CALL cycles.get()
YIELD cycle_id, node;

Example

Step 1: Input graph

Step 2: Cypher load commands

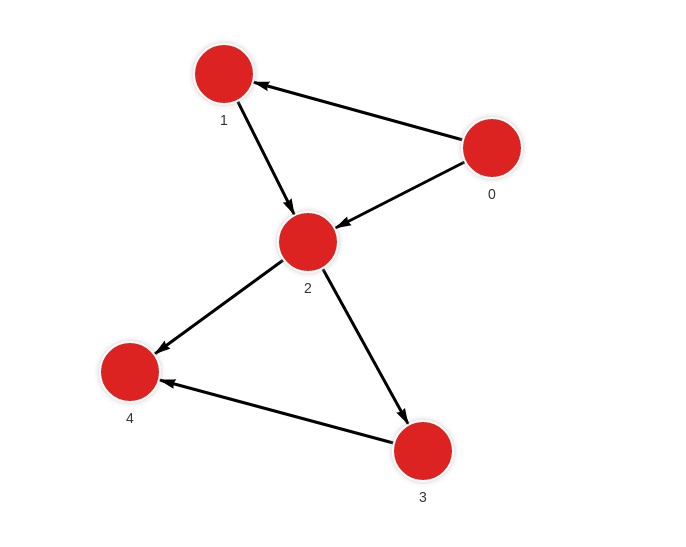
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);

Step 3: Running command

CALL cycles.get()
YIELD cycle_id, node
RETURN cycle_id, node;

Step 4: Results

+-----------------+-----------------+
| cycle_id        | node            |
+-----------------+-----------------+
| 0               | (:Node {id: 2}) |
| 0               | (:Node {id: 0}) |
| 0               | (:Node {id: 1}) |
| 1               | (:Node {id: 4}) |
| 1               | (:Node {id: 2}) |
| 1               | (:Node {id: 3}) |
+-----------------+-----------------+