graph_coloring

Graph coloring is the assignment of colors to nodes such that two nodes connected with an edge don’t have the same color. The goal is to minimize the number of colors while correctly coloring a graph.

Algorithm implementation is inspired by "Quantum Annealing (QA)" ¹, a simple metaheuristic frequently used for solving discrete optimization problems.

QA is a simple strategy for exploring a solution space. The main idea is to start a search with several possible solutions. These solutions change through iterations and produce new “better” solutions. Each solution has a particular error value which depends on the error function that the algorithm optimizes. In the graph coloring scenario, the error function is often defined as the number of edges connecting nodes with the same color.

The algorithm is iterative. It applies several simple rules to change solutions in a loop (the same rules are applied multiple times). The algorithm terminates when a stop criterion is met, usually when the error becomes zero. One of the rules could be to randomly select the node involved in a conflict and change its colors.

Changes made in one iteration may not be permanent if they don’t improve the solution. But, with a certain probability, the new solution is accepted even if its error is not reduced. In that way, the algorithm is prevented from converging to local minimums too early.

¹ Graph Coloring with a Distributed Hybrid Quantum Annealing Algorithm, Olawale TitiloyeAlan Crispin

Trait	Value
Module type	algorithm
Implementation	Python
Graph direction	undirected
Edge weights	weighted/unweighted
Parallelism	parallel

Procedures

info

If you want to execute this algorithm on graph projections, subgraphs or portions of the graph, be sure to check out the guide on How to run a MAGE module on subgraphs.

color_graph(parameters, edge_property)

Input:

• parameters: Dict[string, Any] (default={}) ➡ A dictionary that specifies the algorithm configuration. Configuration parameters are explained in the table below.
• edge_property: string (default=weight) ➡ Edge property that stores the edge weight. Any edge attribute not present defaults to 1.

Output:

• node: Vertex ➡ Represents the node

• color: int ➡ Represents the assigned color

Usage:

CALL graph_coloring.color_graph()
YIELD node, color;

color_subgraph(vertices, edges, parameters, edge_property)

Input:

• vertices: List[Vertex] ➡ List of vertices in the subgraph.
• edges: List[Edge] ➡ List of edges in the subgraph.
• parameters: Dict[string, Any] (default={}) ➡ A dictionary that specifies the algorithm configuration. Configuration parameters are explained in the table below.
• edge_property: string (default=weight) ➡ Edge property that stores the edge weight. Any edge attribute not present defaults to 1.

Output:

• node: Vertex ➡ Represents the node

• color: int ➡ Represents the assigned color

Usage:

MATCH (a)-[e]->(b)
WITH collect(a) as nodes, collect (e) as edges
CALL graph_coloring.color_subgraph(nodes, edges, {no_of_colors: 2})
YIELD node, color;

Parameters

Name	Type	Default	Description
algorithm	String	QA	An optimization strategy used to find graph coloring.
no_of_colors	Integer	10	The number of colors used to color the nodes of the graph.
no_of_processes	Integer	1	The number of processes used to execute the algorithm in parallel.
population_size	Integer	15	The number of different solutions that are improved through iterations.
population_factory	String	ChainChunkFactory	The name of a function that generates an initial population.
init_algorithms	List[String]	[SDO, LDO]	Contains algorithms used to initialize the solutions.
error	String	ConflictError	The name of an error function that is minimized by an optimization strategy.
max_iterations	Integer	10	The maximum number of iterations of an algorithm.
iteration_callbacks	List[String]	[]	Contains iteration callbacks. Iteration callback is called after each iteration of the iterative algorithm. Iteration callback saves certain population information and calls specified actions if certain conditions are met.
communication_delay	Integer	10	The number of iterations that must pass for neighboring parts to exchange solutions.
logging_delay	Integer	10	The number of iteration after the algorithm information is logged.
QA_temperature	Float	0.035	The temperature parameter of the quantum annealing algorithm.
QA_max_steps	Float	10	The maximum number of steps in one iteration.
conflict_err_alpha	Float	0.1	The number that scales the sum of the conflicting edges in the error function formula.
conflict_err_beta	Float	0.001	The number that scales the correlation between solutions in the error function formula.
mutation	String	SimpleMutation	The name of a function that changes the solutions.
multiple_mutation_no_of_nodes	Integer	2	The number of nodes that will change color.
random_mutation_probability	Float	0.1	The probability that the color of the random node (it does not have to be conflicting) will be changed.
simple_tunneling_mutation	String	MultipleMutation	The name of a mutation function.
simple_tunneling_probability	Float	0.5	The probability of changing an individual.
simple_tunneling_error_correction	Float	2	The mutated individual is accepted only if its error is less than the error of the old individual multiplied by this parameter.
simple_tunneling_max_attempts	Integer	25	The maximum number of mutation attempts until the individual is accepted.
convergence_callback_tolerance	Integer	500	The maximum number of iterations in which if the algorithm does not find a better solution convergence occurs and defined actions are called.
convergence_callback_actions	String	[SimpleTunneling]	Actions that are called when convergence is detected.

Example

Step 1: Input graph

Step 2: Cypher load commands

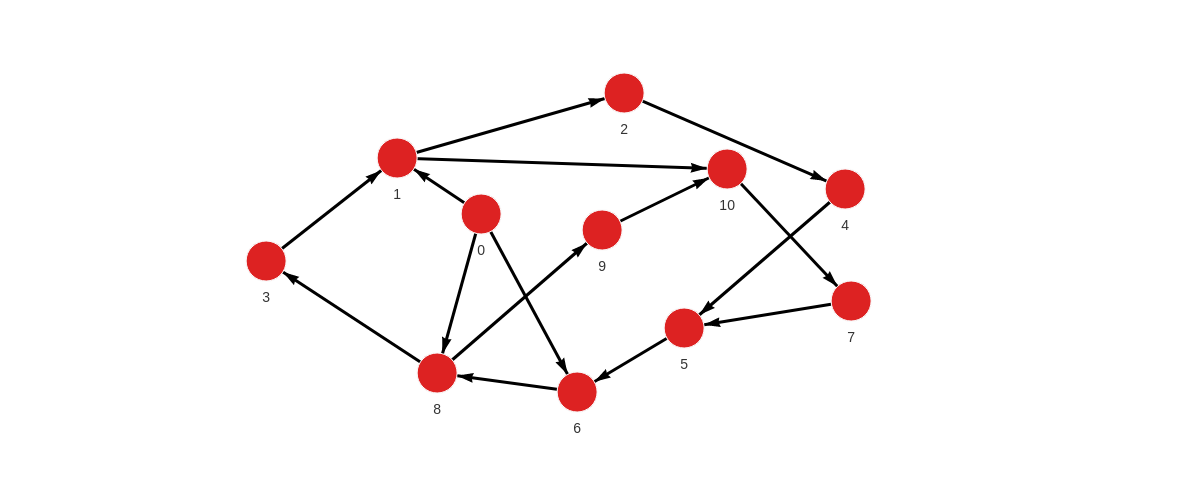
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 6}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 7}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 9}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 9}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 6}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 6}) MERGE (b:Node {id: 8}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 8}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 10}) MERGE (b:Node {id: 7}) CREATE (a)-[:RELATION]->(b);

Step 3: Running command

CALL graph_coloring.color_graph({no_of_colors: 4})
YIELD node, color
RETURN node, color;

Step 4: Results

+-------+-------+
| node  | color |
+-------+-------+
| "130" | "1"   |
| "131" | "3"   |
| "132" | "0"   |
| "133" | "1"   |
| "134" | "2"   |
| "135" | "1"   |
| "136" | "3"   |
| "137" | "0"   |
| "138" | "0"   |
| "139" | "3"   |
| "140" | "1"   |
+-------+-------+