bipartite_matching
A bipartite graph is a graph in which we can divide vertices into two independent sets, such that every edge connects vertices between these sets. No connection can be established within the set. Matching in bipartite graphs (bipartite matching) is described as a set of edges that are picked in a way to not share an endpoint. Furthermore, maximum matching is such matching of maximum cardinality of the chosen edge set. The algorithm runs in O(|V|*|E|) time where V represents a set of nodes and E represents a set of edges.
| Trait | Value |
|---|---|
| Module type | algorithm |
| Implementation | C++ |
| Graph direction | undirected |
| Edge weights | unweighted |
| Parallelism | sequential |
Procedures
info
If you want to execute this algorithm on graph projections, subgraphs or portions of the graph, be sure to check out the guide on How to run a MAGE module on subgraphs.
max()
Output:
maximum_bipartite_matching➡ Maximum bipartite matching, the cardinality of maximum matching edge subset. If graph is not bipartite, zero(0) is returned value.
Usage:
CALL bipartite_matching.max()
YIELD maximum_bipartite_matching;
Example
- Step 1: Input graph
- Step 2: Cypher load commands
- Step 3: Running command
- Step 4: Results
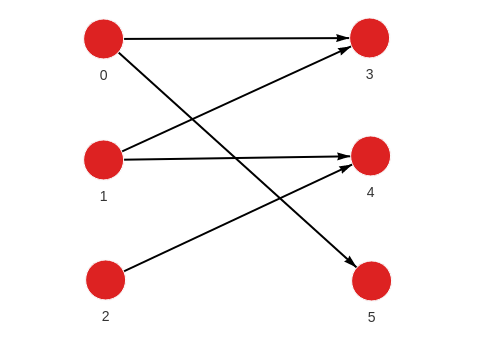
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
CALL bipartite_matching.max()
YIELD maximum_bipartite_matching
RETURN maximum_bipartite_matching;
+----------------------------+
| maximum_bipartite_matching |
+----------------------------+
| 3 |
+----------------------------+
