kmeans

The k-means algorithm clusters given data by trying to separate samples in n groups of equal variance by minimizing the criterion known as within-the-cluster sum-of-squares. To learn more about it, jump to the algorithm page.

Trait	Value
Module type	module
Implementation	Python
Graph direction	directed/undirected
Edge weights	weighted/unweighted
Parallelism	sequential

Too slow?

If this algorithm implementation is too slow for your use case, contact us and request a rewrite to C++ !

Procedures

info

If you want to execute this algorithm on graph projections, subgraphs or portions of the graph, be sure to check out the guide on How to run a MAGE module on subgraphs.

get_clusters(n_clusters, embedding_property, init, n_init, max_iter, tol, algorithm, random_state)

For each node, this procedure returns what cluster it belongs to.

Input:

• n_clusters : int ➡ Number of clusters to be formed.
• embedding_property : str (default: "embedding") ➡ Node property where embeddings are stored.
• init : str (default: "k-means") ➡ Initialization method. If k-means++ is selected, initial cluster centroids are sampled per an empirical probability distribution of the points’ contribution to the overall inertia. This technique speeds up convergence and is theoretically proven to be O(logk)-optimal. If random, n_clusters observations (rows) are randomly chosen for the initial centroids.
• n_init : int (default: 10) ➡ Number of times the k-means algorithm will be run with different centroid seeds.
• max_iter : int (default: 10) ➡ Length of sampling walks.
• tol : float (default: 1e-4) ➡ Relative tolerance of the Frobenius norm of the difference of cluster centers across consecutive iterations. Used in determining convergence.
• algorithm : str (default: "auto") ➡ Options are lloyd, elkan, auto, full. Description here.
• random_state : int (default: 1998) ➡ Random seed for the algorithm.

Output:

• node: mgp.Vertex ➡ Graph node.
• cluster_id: mgp.Number ➡ Cluster ID of the above node.

Usage:

 CALL kmeans.get_clusters(2, "embedding", "k-means++", 10, 10, 0.0001, "auto", 1) YIELD node, cluster_id
 RETURN node.id as node_id, cluster_id
   ORDER BY node_id ASC;

set_clusters( n_clusters, embedding_property, cluster_property, init, n_init, max_iter, tol, algorithm, random_state)

Procedure sets for each node to which cluster it belongs to by writing cluster id to cluster_property.

Input:

• n_clusters : int ➡ Number of clusters to be formed.
• embedding_property : str (default: "embedding") ➡ Node property where embeddings are stored.
• cluster_property: str (default: "cluster_id") ➡ Node property where cluster_id will be stored.
• init : str (default: "k-means") ➡ Initialization method. If k-means++ is selected, initial cluster centroids are sampled per an empirical probability distribution of the points’ contribution to the overall inertia. This technique speeds up convergence and is theoretically proven to be O(logk)-optimal. If random, n_clusters observations (nodes) are randomly chosen for the initial centroids.
• n_init : int (default: 10) ➡ Number of times the k-means algorithm will be run with different centroid seeds.
• max_iter : int (default: 10) ➡ Length of sampling walks.
• tol : float (default: 1e-4) ➡ Relative tolerance of the Frobenius norm of the difference of cluster centers across consecutive iterations. Used in determining convergence.
• algorithm : str (default: "auto") ➡ Options are lloyd, elkan, auto, full. Description here.
• random_state : int (default: 1998) ➡ Random seed for the algorithm.

Output:

• node: mgp.Vertex ➡ Graph node.
• cluster_id: mgp.Number ➡ Cluster ID of the above node.

Usage:

 CALL kmeans.set_clusters(2, "embedding", "cluster_id", "k-means++", 10, 10, 0.0001, "auto", 1) YIELD node, cluster_id
 RETURN node.id as node_id, cluster_id
   ORDER BY node_id ASC;

Example

Step 1: Input graph

Step 2: Load commands

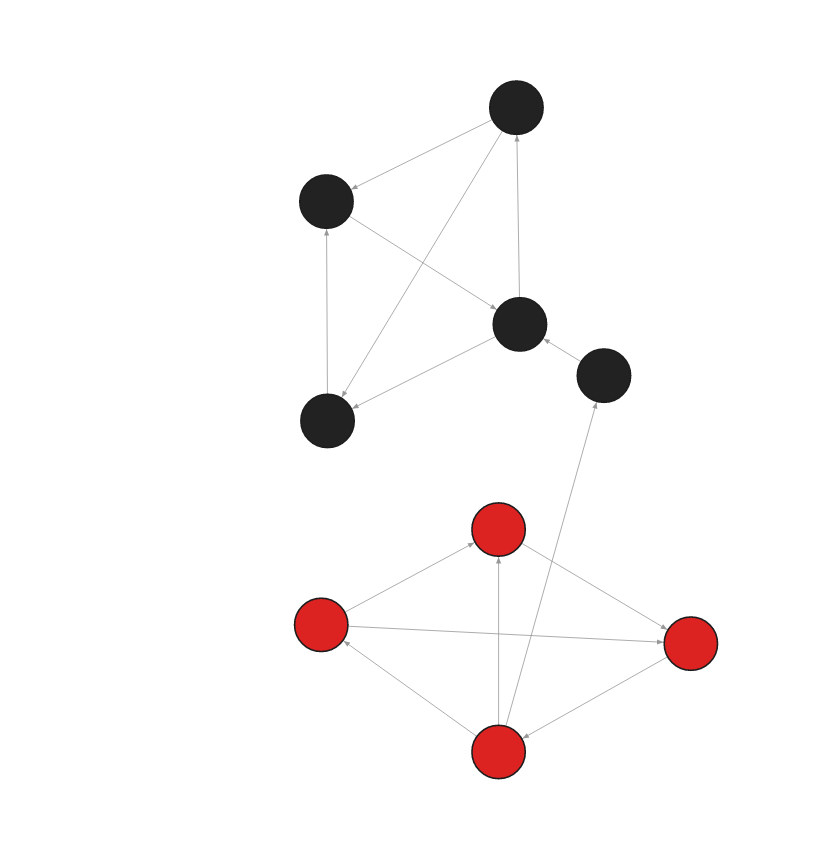
CREATE (:Node {id:0, embedding: [0.90678340196609497, 0.74690568447113037, -0.65984714031219482]});
CREATE (:Node {id:1, embedding: [1.2019195556640625, 0.42643040418624878, -0.4709840714931488]});
CREATE (:Node {id:2, embedding: [1.1005796194076538, 0.67131000757217407, -0.5418705940246582]});
CREATE (:Node {id:4, embedding: [1.1840434074401855, 0.39269298315048218, -0.5063326358795166]});
CREATE (:Node {id:5, embedding: [0.83302301168441772, 0.5545622706413269, -0.31265774369239807]});
CREATE (:Node {id:6, embedding: [0.78877884149551392, 0.5189281702041626, -0.097793936729431152]});
CREATE (:Node {id:7, embedding: [0.61398810148239136, 0.5255049467086792, -0.3551192581653595]});
CREATE (:Node {id:8, embedding: [0.83923488855361938, -0.0041203685104846954, -0.51874136924743652]});
CREATE (:Node {id:9, embedding: [0.60883384943008423, 0.60958302021026611, -0.40317356586456299]});
MATCH (a:Node {id: 0}) MATCH (b:Node {id: 1}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 1}) MATCH (b:Node {id: 2}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 2}) MATCH (b:Node {id: 0}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 0}) MATCH (b:Node {id: 4}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 4}) MATCH (b:Node {id: 1}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 4}) MATCH (b:Node {id: 2}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 0}) MATCH (b:Node {id: 5}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 5}) MATCH (b:Node {id: 6}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 6}) MATCH (b:Node {id: 7}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 7}) MATCH (b:Node {id: 8}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 8}) MATCH (b:Node {id: 6}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 6}) MATCH (b:Node {id: 9}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 9}) MATCH (b:Node {id: 7}) MERGE (a)-[:RELATION]->(b);
MATCH (a:Node {id: 9}) MATCH (b:Node {id: 8}) MERGE (a)-[:RELATION]->(b);

Step 3: Get clusters

CALL kmeans.get_clusters(2, "embedding", "k-means++", 10, 10, 0.0001, "auto", 1) YIELD node, cluster_id
  RETURN node.id as node_id, cluster_id
  ORDER BY node_id ASC;

Step 4: Results

+-------------------------+-------------------------+
| node_id                 | cluster_id              |
+-------------------------+-------------------------+
| 0                       | 1                       |
| 1                       | 1                       |
| 2                       | 1                       |
| 4                       | 1                       |
| 5                       | 0                       |
| 6                       | 0                       |
| 7                       | 0                       |
| 8                       | 0                       |
| 9                       | 0                       |
+-------------------------+-------------------------+