community_detection
This query module enables using the Louvain method[1] for community detection, using the Grappolo parallel implementation.
The Louvain algorithm belongs to the modularity maximization family of community detection algorithms. Each node is initially assigned to its own community, and the algorithm uses a greedy heuristic to search for the community partition with the highest modularity score by merging previously obtained communities.
The algorithm is suitable for large-scale graphs as it runs in O(nlogn) time on a graph with n nodes. Further performance gains are obtained by parallelization using a distance-1 graph coloring heuristic, and a graph coarsening algorithm that aims to preserve communities.
1 Fast unfolding of communities in large networks, Blondel et al.
| Trait | Value |
|---|---|
| Module type | algorithm |
| Implementation | C++ |
| Graph direction | undirected |
| Relationship weights | weighted / unweighted |
| Parallelism | parallel |
Procedures
If you want to execute this algorithm on graph projections, subgraphs or portions of the graph, be sure to check out the guide on How to run a MAGE module on subgraphs.
get(weight, coloring, min_graph_shrink, community_alg_threshold, coloring_alg_threshold)
Computes graph communities using the Louvain method.
Input
weight: string (default=null)➡ Specifies the default edge weight. If not set, the algorithm uses theweightedge attribute when present and otherwise treats the graph as unweighted.coloring: boolean (default=False)➡ If set, use the graph coloring heuristic for effective parallelization.min_graph_shrink: integer (default=100000)➡ The graph coarsening optimization stops upon shrinking the graph to this many nodes.community_alg_threshold: double (default=0.000001)➡ Controls how long the algorithm iterates. When the gain in modularity goes below the threshold, iteration is over. Valid values are between 0 and 1 (exclusive).coloring_alg_threshold: double (default=0.01)➡ If coloring is enabled, controls how long the algorithm iterates. When the gain in modularity goes below this threshold, a final iteration is performed using thecommunity_alg_thresholdvalue. Valid values are between 0 and 1 (exclusive); this parameter's value should be higher thancommunity_alg_threshold.
Output
node: Vertex➡ Graph node.community_id: integer➡ Community ID. Defaults to -1 if the node does not belong to any community.
Usage
CALL community_detection.get()
YIELD node, community_id;
get_subgraph(subgraph_nodes, subgraph_relationships, weight, coloring, min_graph_shrink, community_alg_threshold, coloring_alg_threshold)
Computes graph communities over a subgraph using the Louvain method.
Input
subgraph_nodes: List[Node]➡ List of nodes in the subgraph.subgraph_relationships: List[Relationship]➡ List of relationships in the subgraph.weight: str (default=null)➡ Specifies the default relationship weight. If not set, the algorithm uses theweightrelationship attribute when present and otherwise treats the graph as unweighted.coloring: bool (default=False)➡ If set, use the graph coloring heuristic for effective parallelization.min_graph_shrink: int (default=100000)➡ The graph coarsening optimization stops upon shrinking the graph to this many nodes.community_alg_threshold: double (default=0.000001)➡ Controls how long the algorithm iterates. When the gain in modularity goes below the threshold, iteration is over. Valid values are between 0 and 1 (exclusive).coloring_alg_threshold: double (default=0.01)➡ If coloring is enabled, controls how long the algorithm iterates. When the gain in modularity goes below this threshold, a final iteration is performed using thecommunity_alg_thresholdvalue. Valid values are between 0 and 1 (exclusive); this parameter's value should be higher thancommunity_alg_threshold.
Output
node: Vertex➡ Graph node.community_id: int➡ Community ID. Defaults to -1 if the node does not belong to any community.
Usage
MATCH (a)-[e]-(b)
WITH COLLECT(a) AS nodes, COLLECT (e) AS relationships
CALL community_detection.get_subgraph(nodes, relationships)
YIELD node, community_id;
Example
- Step 1: Input graph
- Step 3: Load commands
- Step 4: Running command
- Step 5: Results
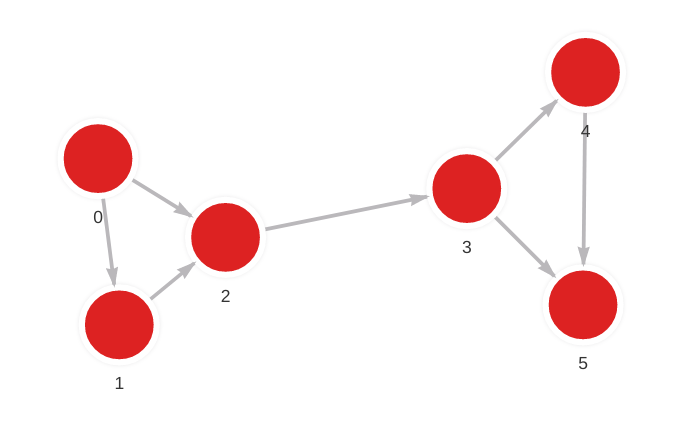
MERGE (a: Node {id: 0}) MERGE (b: Node {id: 1}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 0}) MERGE (b: Node {id: 2}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 1}) MERGE (b: Node {id: 2}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 2}) MERGE (b: Node {id: 3}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 3}) MERGE (b: Node {id: 4}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 3}) MERGE (b: Node {id: 5}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 4}) MERGE (b: Node {id: 5}) CREATE (a)-[r: Relation]->(b);
CALL community_detection.get()
YIELD node, community_id
RETURN node.id AS node_id, community_id
ORDER BY node_id;
┌─────────────────────────┬─────────────────────────┐
│ node_id │ community_id │
├─────────────────────────┼─────────────────────────┤
│ 0 │ 1 │
│ 1 │ 1 │
│ 2 │ 1 │
│ 3 │ 2 │
│ 4 │ 2 │
│ 5 │ 2 │
└─────────────────────────┴─────────────────────────┘
