PERCENTILEedit
The value at which a certain percentage of observed values occur. For example,
the 95th percentile is the value which is greater than 95% of the observed values and
the 50th percentile is the MEDIAN.
FROM employees
| STATS p0 = PERCENTILE(salary, 0)
, p50 = PERCENTILE(salary, 50)
, p99 = PERCENTILE(salary, 99)
| p0:double | p50:double | p99:double |
|---|---|---|
25324 |
47003 |
74970.29 |
PERCENTILE is (usually) approximateedit
There are many different algorithms to calculate percentiles. The naive
implementation simply stores all the values in a sorted array. To find the 50th
percentile, you simply find the value that is at my_array[count(my_array) * 0.5].
Clearly, the naive implementation does not scale — the sorted array grows linearly with the number of values in your dataset. To calculate percentiles across potentially billions of values in an Elasticsearch cluster, approximate percentiles are calculated.
The algorithm used by the percentile metric is called TDigest (introduced by
Ted Dunning in
Computing Accurate Quantiles using T-Digests).
When using this metric, there are a few guidelines to keep in mind:
-
Accuracy is proportional to
q(1-q). This means that extreme percentiles (e.g. 99%) are more accurate than less extreme percentiles, such as the median - For small sets of values, percentiles are highly accurate (and potentially 100% accurate if the data is small enough).
- As the quantity of values in a bucket grows, the algorithm begins to approximate the percentiles. It is effectively trading accuracy for memory savings. The exact level of inaccuracy is difficult to generalize, since it depends on your data distribution and volume of data being aggregated
The following chart shows the relative error on a uniform distribution depending on the number of collected values and the requested percentile:
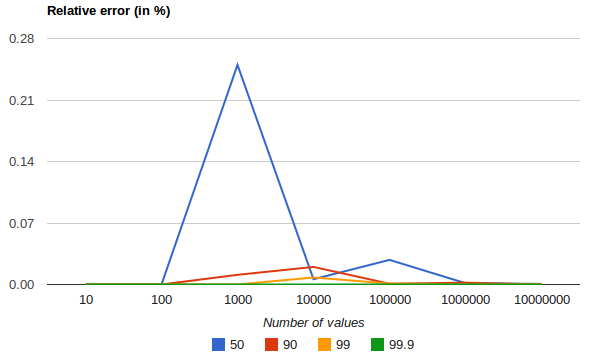
It shows how precision is better for extreme percentiles. The reason why error diminishes for large number of values is that the law of large numbers makes the distribution of values more and more uniform and the t-digest tree can do a better job at summarizing it. It would not be the case on more skewed distributions.
PERCENTILE is also non-deterministic.
This means you can get slightly different results using the same data.